Un QCM de Mathématiques complet pour vous aider à vous améliorer !

#1. L’entrepôt dont l’aire est supérieure à 150 m² est :
– Entrepôt A : aire d’un carré = côté x côté ; soit 12×12 = 144m²
– Entrepôt B : aire d’un rectangle = longueur x largeur ; soit 8×15 = 120m²
– Entrepôt C : aire d’un cercle = Pi x rayon au carré ;
rayon = diamètre / 2 = 12 / 2 = 6 ;
Aire entrepôt C = 3,14 x 6² = 113,04m²
– Entrepôt D : périmètre d’un carré = 4 x longueur des côtés ; 1 côté a une longueur de : 40/4 = 10m ;
Aire du carré = côté x côté = 10×10 = 100m²
#2. Quel est le Plus Grand Commun Diviseur (PGCD) de 24 et de 18 ?
Algorithme d’Euclide
24 / 18 = 1 reste 6
18 / 6 = 3 reste 0
Le PGCD est le dernier reste non nul, soit 6.
Ainsi, PGCD (24 ; 18) = 6
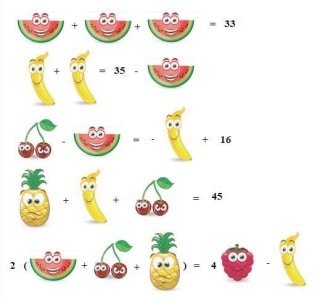
#3. Les fruits suivants contiennent tous de la vitamine C. Si :
→ 3 pastèques = 33 ; 1 pastèque = 11
→ 2 bananes = 35 – 11 = 24; 1 banane = 12
→ 1 cerise – 11 = – 12 +16 = 4 ; 1 cerise = 4 + 11 = 15
→ 1 ananas 12 + 15 = 45 ; 1 ananas = 45 – 12 – 15 = 18
→ 2 (11 + 15 + 18) = 4 framboises – 12
88 = 4 framboises – 12
4 framboises = 88 + 12 = 100
1 framboise = 100/4 = 25

#4. Quelle est la valeur de i pour n=3 ?
Il faut suivre les instructions de l’algorithme :
– À l’initialisation, i = 5 et n = 1 et tant que i < 100, signifie tant que i = 5 < 100.
À cette étape, il faut calculer la valeur de « i » : i x 3/2 soit 5 x 3/2 = 15/2 = 7,5
Ensuite on calcule la valeur de « n » : n 1 = 1 1 = 2.
– Puis on répète l’opération :
Tant que i < 100 correspond maintenant à i = 7,5 < 100 ; et désormais n = 2
On calcule la valeur de « i » : i x 3/2, soit 7,5 x 3/2 = 22,5/2 = 11,25
On calcule la valeur de « n » : n 1 = 2 1 = 3.
→ Ainsi pour n = 3, i = 11,25
#5. Camille souhaite enduire les murs et les plafonds de son studio qui mesure 4m de long, 6m de large et 2,5m de haut. Un pot de 10 kg de peinture permet de couvrir 15m². Combien de pots faut-il ?
– Surface totale des 4 murs : 2x(longueur x hauteur) + 2x(largeur x hauteur) = 2x(4×2,5) + 2x(6×2,5) = 20 + 30 = 50 m²
– Surface totale du plafond : longueur x largeur = 6 x4 = 24 m²
→ surface totale à peindre : 50 + 24 = 74 m²
Nombre de pots de peinture pour l’appartement de Camille : 1 pot couvre 15 m²
74/15 = 4,93, arrondi à l’entier supérieur = 5 pots de peinture.
#6. Factorisez l’équation suivante : 25(x-6)² - 49
a² – b² = (a-b)(a+b)
25(x-6)² – 49
= [5(x-6)]² – 7² → a = 5(x-6) et b = 7
= [5(x-6) – 7] [5(x-6) + 7]
= (5x – 30 – 7)(5x – 30 + 7)
= (5x-37)(5x-23)
#7. 500 ml de lait contiennent 600 mg de calcium, soit 75 % de l'apport quotidien recommandé pour un adulte. En consommant 125 ml de lait, quelle est la quantité de calcium absorbée ?
500 ml de lait contient 600 mg de calcium
Pour 125 ml de lait on absorbe : 125×600 / 500 = 75 000 / 500 = 150 mg de calcium
#8. Pour arriver à destination, un train doit rouler durant 4 heures et 47 minutes et s’arrêter 6 fois pour une durée moyenne de 4 minutes. Quelle est son heure d’arrivée, sachant que son heure de départ est 8 h 56 ?
Le train part à 8h56
Le train effectue 6 arrêts de 4 minutes : 6×4 = 24 minutes
Le trajet est de 4h47 + 24 ; soit 5h11
L’arrivée est prévue à 8h56 + 5h11 = 14h07 !
#9. Combien vaut -(3)^5 ?
-(3)^5 = – 3x3x3x3x3 = -243
#10. Quel est le bon résultat : 75 cm + 13 mm ?
Il faut convertir les longueurs sous la même unité :
75 cm = 750 mm
750mm+ 13mm = 763 mm soit 7,63 dm
#11. Sur un plan à l'échelle 1/1500, une parcelle cadastrale est représentée par un rectangle de 4,5 cm de longueur et 0,8 cm de largeur. Quelle est sa superficie réelle en m² ?
Aire rectangle = longueur x largeur = (1 500×4,5) x (0,8×1 500) = 6 750 x 1 200 = 8 100 000 cm²
soit 810m²
#12. Tristan souhaite bétonner le chemin d'accès à sa maison, assimilé à une bande rectangulaire de 5m de largeur sur 50m de longueur, épaisse de 10 cm. Pour fabriquer 1m3 de béton, on utilise en moyenne 8 sacs de 35kg de ciment. Quelle masse de ciment Tristan devra-t-il se faire livrer pour bétonner tout son chemin ?
– épaisseur 10cm = 0,1m
– volume à bétonner : longueur x largeur x épaisseur = 50x5x0,1 = 25m3
– masse de ciment = 25x(8×35) = 7 000 kg soit 7 tonnes (1 tonne = 1 000 kg)

#13. En fonction des vitesses maximales des quatre véhicules ci-dessous sur circuit, indiquez lequel est le plus rapide :
– la Formule 3000 parcourt 4 kilomètres en 1 minute : 4x60km en 1 heure = 240 km/h
– la Moto Grand Prix a une vitesse de pointe de 305 km/h
– le TGV met une demi-heure pour parcourir 161 kilomètres : 2×161 = 322 km/h
– l’ULM multi-axe vole à 80 mètres à la seconde : 80×3600 = 288 000 m/h = 288 km/h
#14. Lequel de ces chiffres n’est pas un nombre premier ?
Un nombre premier est un nombre qui est divisible uniquement par lui-même et par 1.
Or, 3 x 3 = 9 donc 9 est divisible par 3.
#15. Une personne détenant le quart de la valeur d’une maison décide de la partager équitablement entre ses cinq héritiers. Quelle part de la maison reviendra à chaque héritier ?
La personne détient 1/4 de la valeur d’un immeuble.
Elle partage ce quart entre ses 5 héritiers.
Chaque héritier va donc recevoir 1/5ème d’1/4 de la valeur de l’immeuble, soit : 1/4 x 1/5 = 1/20ème
#16. Dans un jardin, une piscine extérieure de forme cylindrique avec une hauteur de 2 mètres et un diamètre de 8 mètres, est remplie au 2/3. Quel volume d’eau y a-t-il dans la piscine (arrondi à l’entier le plus proche) ? Pi = 3,14
Formule du volume d’un cylindre = Pi x r x r x H
Diamètre = 8 ; rayon = diamètre / 2 = 8/2 = 4m
Hauteur = 2 x 2/3 = 4/3 = 0,75m
Volume du cylindre = 3,14 x 4 x 4 x 0,75 = 100,48m3
La piscine est remplie au 2/3 soit 100,48 x 2/3 = 66,98 arrondi à l’entier supérieur 67 m³

#17. Un appareil de lecture sélectionne au hasard un des huit morceaux. Quelle est la probabilité d’écouter un morceau d’au moins 220 secondes ?
A la queue leu leu = 280 secondes
Je te survivrai = 4 minutes → 4 x 60 secondes = 240 secondes
Nuit de folie = 260 secondes
La lambada = 200 secondes
Jolie poupée = 4 minutes et 20 secondes → 240 + 20 = 260 secondes
Une autre histoire = 240 secondes
La danse des canards = 3 minutes et 20 secondes → 3 x 60 secondes + 20 = 200 secondes
Big bisous = 280 secondes
Sur les 8 morceaux de musique, 6 durent plus de 220 secondes. Il existe donc 6 chances sur 8 (6/8) soit 3 chances sur 4 (3/4) d’écouter un morceau d’au moins 220 secondes.
#18. Soit ABC un triangle rectangle en A ; D est l’image symétrique de C par rapport à la droite AB. Quelle est la nature du triangle BDC ?
Les deux triangles sont identiques.
En les positionnant côte à côte, ils forment un triangle isocèle.
#19. D’un montant de 388 euros, la taxe d’habitation de l'année 2017 a augmenté de 5 % par rapport à celle de l'année 2015, qui elle-même était inférieure de 2 % à celle de l'année suivante. Quel était le montant approximatif de la taxe d'habitation de l'année 2016 ?
TH 2017 = 388 €
TH 2015 = TH 2017 (– 5 %) = 388/1,05 = 369,58 €
TH 2016 = TH 2015 (+ 2 %) = 369,58 x 0,02 = 7,39 → 369,58 + 7,39 = 376,97 €
#20. Le point O est donné et k = -1/3 ; M' est l’image de M par l’homothétie de centre O et de rapport -1/3
M’ est l’image de M par l’homothétie de centre O et de rapport k = – 1/3
OM et OM’ sont colinéaires avec le point O en commun. Par conséquent, les points MOM’ sont alignés.
#21. Camille et Arthur mangent des bonbons. Camille a mangé 3/8 du paquet de bonbons et Arthur les 7/9 de ce qu’il restait. Sachant qu’il reste 95g dans le paquet, quelle était la masse du paquet de bonbons avant qu’Arthur et Camille ne les mangent.
P : poids du paquet de bonbons neuf
Camille a mangé 3/8 du paquet ; il reste 5/8 du total des bonbons
Arthur a mangé 7/9 des 5/8ème restants. Il reste donc 2/9ème des 5/8ème, soit 10/72ème ou encore 5/36ème. Avec l’énoncé on sait que 5/36ème du paquet = 95 grammes.
On calcule combien de grammes il y a dans 1/36ème du paquet de bonbons = 95 / 5 = 19 grammes
P = 19g x 36 = 684g
#22. Pour remplir sa piscine, Monsieur Berger dispose d’un tuyau d’arrosage avec un débit de 3,5 litres d’eau par minute. Il laisse couler l’eau pendant 4h35 min. Combien faudra-t-il encore de litres d’eau pour remplir cette piscine qui a une contenance de 1,5 m³ ?
Eau déversée en 4h35 = 3,5 x (4×60 + 35) = 962,5 litres
1L = 1dm3
962,5 L = 962,5 dm 3 → 0,9625 m³
Il faut donc : 1,5 m³ – 0,9625 m³ = 0,5375 m³ → 537,50 dm³ soit 537,5 litres d’eau pour remplir la piscine.
#23. Quel est le résultat de l’opération suivante : 37/36 + 1/3 - 5/12 = ?
Il faut un dénominateur commun pour additionner et soustraire ces équations :
37/36 + 12/36 – 15/36 = 34/36 = 17/18
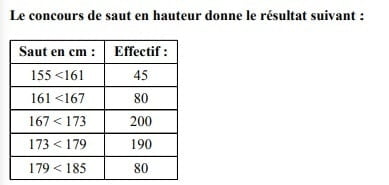
#24. Quelle est la classe modale ?
Une classe modale est une série où la fréquence est la plus élevée.
Dans l’exemple, il y a 200 personnes qui ont réussi un saut en hauteur entre 167 et 173 cm.
#25. Monsieur Legal bénéficie d’une remise de 25% sur une pendulette d’une valeur de 15 €. Combien va-t-il la payer ?
Montant à payer 15 x 0,75 = 11,25 euros
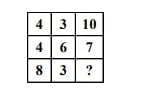
#26. Complétez le tableau ci-dessus :
En additionnant les chiffres des 2 premières lignes le résultat est égal à 17.
Il faut donc trouver le chiffre qui permettra d’obtenir 17, soit ? = 17 – 8 – 3 = 6
#27. Trouvez la suite : C49 – G121 – K364 – ?
Pour trouver la lettre, il faut sauter 3 lettre à chaque série :
C (DEF) G (HIJ) K (LMN) O
Vérifions la suite logique avec le nombre :
49 → 4 9 = 13 → 1 3 = 4
121 → 1 2 1 = 4
364 → 3 6 4 = 13 → 1 3 = 4
Propositions de l’énoncé :
454 → 4 5 4 = 13 → 1 3 = 4
453 → 4 5 3 = 12 → 1 2 = 3
76 → 7 6 = 13 → 1 3 = 4
83 → 8 3 = 11 → 1 1 = 2
#28. Un triangle a trois angles. Un petit, un moyen qui est le double du petit et un grand qui est le triple du petit. Il s’agit donc :
La somme des angles d’un triangle est de 180°, soit angle 1 + angle 2 + angle 3 = 180°
D’après l’énoncé :
angle 2 = 2 x angle 1
angle 3 = 3 x angle 1
Ainsi, angle 1 + angle 2 + angle 3 = 180° équivaut à angle 1 + 2 x angle 1 + 3 x angle 1 = 180°
Soit : 6 X angle 1 = 180°
Donc : angle 1 = 180° / 6 = 30°
On reprend les formules de l’énoncé :
angle 2 = 2 x angle 1 = 2 x 30° = 60°
angle 3 = 3 x angle 1 = 3 x 30° = 90° → le triangle ayant un angle à 90°, il s’agit d’un triangle rectangle.
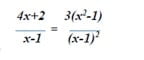
#29. Quelle est la solution de l'équation suivante ?
En remplaçant dans l’énoncé « x » par les solutions proposées, on s’aperçoit que seule la proposition n°3 fonctionne : x = 1
#30. La moyenne d'un élève sur 4 épreuves est de 13/20. Quelle doit être sa note à la 5ème épreuve pour obtenir une moyenne de 14/20 ?
– Moyenne actuelle = 13/20
– Soit 13 x 4 = 52 points
– Pour obtenir une moyenne de 14/20, en 5 épreuves, l’élève doit obtenir 14 x 5 = 70 points
– Note à avoir au prochain devoir = 70 – 52 = 18/20
#31. Trois personnes achètent ensemble un cheval de course. Le premier met le tiers du prix, le second met 45 % de la somme et le dernier met 13 000 €. Combien coûte ce cheval ?
On reprend l’énoncé :
1ère personne (A) : 1/3 du prix = 33,33 %
2ème personne (B) : 45 % du prix
3ème personne (C) : 13 000 euros
Ainsi, A + B ont payé 45% + 33,33% = 78,33 % du prix.
Les 13 000 euros payés par C représentent 21,67 % du prix.
Pour connaître le prix du cheval on effectue un produit en croix :
Prix du cheval = 100 %
13 000 € = 21,67 %
Donc le prix du cheval = (13 000 x 100) / 21,67 = 60 000 euros.
#32. Trouvez la figure qui possède la plus grande surface parmi les quatre propositions suivantes :
L’aire est la mesure de la surface en m²
– Surface d’un cercle : Pi x rayon²
Surface du cercle = 3,14 x 2² = 3,14 x 4 = 12,56 cm²
– Surface d’un triangle rectangle : multiplication de la longueur des 2 côtés formant l’angle droit divisé par 2
Surface du triangle rectangle = (6 x 4) / 2 = 12 cm²
– Surface d’un carré : côté x côté
Surface du carré = 4,5 x 4,5 = 20,25 cm²
– Surface d’un rectangle : Longueur x largeur
Surface du rectangle = 6 x 3 = 18 cm²
#33. Supposons un nouveau système de numérotation dans lequel 1 heure ferait 70 minutes et 1 minute ferait 40 secondes. À quelle durée en heure / minutes / secondes correspondrait une durée de 4 500 secondes ?
On pose les formules de l’énoncé :
– 1 heure = 70 minutes
– 1 minute = 40 secondes
Puis, on calcule combien de secondes il y a dans 1 heure : 70 x 40 = 2 800 secondes
Il reste donc 4 500 – 2 800 = 1 700 secondes
1 700 / 40 = 42,5
Ainsi, avec cette hypothèse 4 500 secondes correspondent à 1heure 42 minutes et 20 secondes
#34. L'équation (2x + 3)² − (2x − 3)² est égale à :
Identités remarquables :
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
On applique les formules à l’énoncé :
(2x + 3)² − (2x − 3)²
→ 4x² + 12x + 9 – (4x² – 12x + 9)
→ 4x² + 12x + 9 – 4x² + 12x – 9
→ 24x
#35. Pierre doit renouveler l’eau de son aquarium de 120 cm de longueur, 50 cm de largeur et 60 cm de hauteur. En combien de temps sera-t-il rempli avec un robinet qui a un débit de 0,5 litre par seconde ?
Volume d’un rectangle :
Longueur x largeur x hauteur = 120 x 50 x 60 = 360 000 cm³, soit 360 dm³
1 Litre = 1 dm³
L’aquarium se remplit de 0,5 L par seconde.
Avec notre calcul, on sait que l’aquarium sera plein lorsqu’il y aura 360 L.
Temps pour remplir l’aquarium = nombre de litre / débit = 360 / 0,5 = 720 secondes ;
1 minute = 60 secondes ; 720 / 60 = 12 minutes
#36. En période de soldes, un téléphone au prix de 420 euros bénéficie d'une remise de 30 % et sa coque de protection au prix de 22 euros d'un rabais de 50 %. Quel sera, à l'euro supérieur, le prix de l'ensemble après application d'une remise complémentaire de 5 % ?
Prix initial du téléphone = 420 euros
Prix soldé = prix initial – 30 % = 420 x 0,70 = 294 euros
Prix initial de la coque de protection = 22 euros
Prix soldé de la coque de protection = prix initial – 50 % = 22 / 2 = 11 euros
Prix soldé du téléphone + prix soldé de la coque de protection = 294 + 11 = 305 euros
Remise supplémentaire de 5 % sur l’ensemble : 305 x 0,95 = 290 euros
#37. Quelle est la solution de l’inéquation suivante ? (-2x + 3)(x-5) ≥ 0
Remplaçons « x » par « 3/2 » et « 5 », on trouve 0
Si on remplace par 1 on trouve un nombre négatif : l’équation serait fausse et donc les 3 premières propositions sont à exclure.
#38. Combien vaut l'équation ci-dessus ?
1ère étape : on simplifie l’équation :
– on trouve des numérateurs et des dénominateurs communs : (24 x 35 x 99) / (4 x 9 x 30) = (4 x 6 x 5 x 7 x 9 x 11) / (4 x 9 x 6 x 5)
– on supprime les numérateurs et dénominateurs communs : (4 x 6 x 5 x 7 x 9 x 11) / (4 x 9 x 6 x 5) = 7 x 11
2ème étape : on calcule : 7 x 11 = 77
#39. Soit un triangle rectangle dont les côtés adjacents à l’angle droit ont des longueurs de : L = 80 cm l = L - 70 mm. Calculez sa surface :
Surface d’un rectangle = (Longueur x largeur)/2 = [80 x (80 – 7 )]/2 = (80 x 73)/2 = 2 920 cm²
#40. Simplifiez M
√294 = 7 x 7 x 6
M = √294 x 1√6 = 7√6 / √6 = 7

#41. Répondre à la question ci-dessus :

#42. Combien de tickets à tarif réduit ont été délivrés ?
Recette totale = 311 euros
Prix :
Plein tarif = 8 euros ; tickets 573 à 603, soit 31 tickets = 31 x 8€ = 248 euros
Super réduit = 1 euro ; tickets 112 à 119, soit 8 tickets = 8 x 1€ = 8 euros
Réduit = 5 euros ; X tickets : 311€ – 248€ – 8€ = 55€ / 5 = 11 tickets
#43. Résolvez l'addition suivante : 6 h 37 min 58 s + 2 h 22 min 25 s + 1 h 08 min 56 s
Il faut additionner les heures, les minutes et les secondes à part :
Heures : 6 + 2 + 1 = 9 heures
Minutes : 37 + 22 + 8 = 67 minutes, soit 01h07
Secondes : 58 + 25 + 58 = 139 secondes, soit 2 minutes et 19 secondes
Soit : 10 heures, 9 minutes et 19 secondes
#44. Vous souhaitez acheter le plus grand champ parmi 4 qui vous sont proposés. Lequel choisissez vous parmi les propositions suivantes ?
1. Calcul de la surface du terrain en forme de rectangle = L x l = 540m x 300m = 162 000m2, soit 16,2 hectares.
2. Terrain de 16 hectares
3. Calcul de la surface du terrain en forme de triangle : B x h / 2 = 600×500/2 = 150 000 m2, soit 15 hectares.
4. 0,16km2 = 16 hectares

#45. Quelle est la formule la plus économique pour cet étudiant ?
Son stage dure 3 semaines au cours desquelles il va se déplacer 3 jours/semaine. Il va donc se déplacer 3 x 3 = 9 fois, multiplié par 2 pour prendre en compte les allers-retours = 9 x 2 = 18 trajets.
18 tickets à l’unité = 18 x 2 = 36 euros
Carnet de 10 tickets = 16 + 16 = 32 euros
Abonnement hebdomadaire = 15 x 3 = 35 euros
Abonnement mensuel = 40 euros
#46. Lors d'une élection, on a relevé un taux d'abstentionnistes de 25%. Le candidat A a été élu face au candidat B avec 60% des voix des votants. On dénombre, dans le pays, 40 millions d'inscrits sur les listes électorales. Quelle affirmation est exacte ?
40 millions d’inscrits sur les listes électorales
25 % d’abstentionnistes = 40Mx25 % = 10 millions d’électeurs,
Soit 30 millions d’électeurs (40M – 10M)
60 % des votes pour le candidat A = 30×60 % = 18 millions de voix → 45 % des inscrits
#47. Si la tangente d'un angle  est de 1, quelle est la valeur de cet angle ?
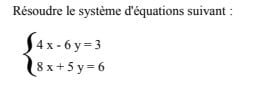
#48. Résoudre le système d'équations suivant :
4x – 6y = 3 donc x = 6/4y + 3 = 3/2x + 3/4
8x + 5y = 6
On remplace x par 3/2x + 3/4 dans la seconde équation
soit 8x + 5y = 6 → 8 (3/2x + 3/4) 5y = 6 → 24/2y + 24/4 +5y = 6 → 12y + 5 y = 6 – 6
→ 17y = 0
#49. Soit ABC un triangle dont les 3 sommets sont des points inscrits dans un cercle de centre O. [BC] est le diamètre du cercle. AB = 3 et AC = 4. Calculez le rayon du cercle de centre O.
Théorème de Pythagore
BC² = AB² + AC² = 3² + 4² = 9 + 16 = 25
BC = 5
Le diamètre est égal à 5
Le rayon = 5/2 = 2,5
#50. Un élève a obtenu 15/20 coefficient 3, 8/20 coefficient 1, 16,50/20 coefficient 4 et 13/20 coefficient 2. Quelle est sa moyenne ?
Moyenne = (3×15 + 1×8 + 4x 16,5 + 2×13) / (3 + 1 + 4 + 2) = 145 / 10 = 14,50
#51. Dans un sac, il y a 9 billes au total : 4 billes rouges, 2 billes bleues et 3 billes jaunes. Quelle est la probabilité de tirer une bille jaune suivie d'une bille rouge ?
(3/9)x(4/8) = 12/72 = 1/6
#52. Le prix d'un kilogramme de beurre est passé de 35 centimes d'euros à 38 centimes d'euros entre 2012 et 2018. Quel est son pourcentage d'augmentation arrondi au dixième près ?
Le taux d’augmentation est de : (0,38 – 0,35) / 0,35 = 0,0857 soit 8,60%
#53. Un maraîcher a planté 25 ares de pieds de tomates à raison de quatre pieds par mètre carré. Le rendement moyen est de cinq kilogrammes par pieds. La sécheresse a réduit les rendements moyens de 20 %. Combien de tonnes de tomates le maraîcher va-t-il récolter ?
1 are = 100 m²
25 ares = 2 500 m²
4 pieds de tomates par m²
4 pieds de tomates x 2 500 m² = 10 000 pieds de tomates
5kg par pieds de tomates
5kg x 10 000 pieds de tomates = 50 000 kg
En raison de la sécheresse, le rendement a diminué de 20 % : 50 000 x 0,20 = 10 000kg
La récolte après la sécheresse est de 50 000 – 10 000 = 40 000kg, soit 40 tonnes.
#54. Un jardin circulaire a un diamètre de 3,50 m. Quelle est l'aire du jardin arrondie au dixième près ?
Aire d’un cercle = Pi x r²
Le rayon est de : diamètre / 2 ; soit : 3,50 / 2 = 1,75
Ainsi, l’aire du jardin = 3,14 x (1,75×1,75) = 9,616
- Arrondi au dixième = 9,6 m²
- Arrondi au centième = 9,62 m²
#55. Sous quelle forme factorisée s'écrit : 25x² + 20x - 12 ?
(5x + 6) (5x – 2) = 25x² – 10x + 30x – 12 = 25x² + 20x – 12
#56. Thomas vit à Poitiers et Antoine à Paris. Ils se donnent rendez-vous à Tours. Paris est à 240 km de Tours et à 340 km de Poitiers. Thomas, qui ne prend jamais l'autoroute, roule à une vitesse moyenne de 50 km/h. Antoine, lui, prend l'autoroute ; mais, compte tenu de la circulation, il roule à une vitesse moyenne de 100 km/h, au lieu des 130km/h autorisés. S'ils partent tous les deux à la même heure, lequel des deux arrive le premier à Tours et combien de temps doit-il attendre son ami ?
Thomas : Poitier – Tours = 340 – 240 = 100 km ; 50km/h
Antoine : Paris – Tours = 240km ; 100 km/h
Vitesse = distance / temps ; ainsi temps = distance / vitesse
Temps de trajet de Thomas : 100 / 50 = 2 heures
Temps de trajet d’Antoine : 240 / 100 = 2,4 heures
Thomas arrivera en premier.
Thomas attendra Antoine 24 minutes (1 heure = 60 minutes ; donc (0,40 x 60) / 1 = 24 minutes
#57. Une mere souhaite répartir 160 € d'argent de poche entre ses trois fils, Orène (l'aîné), Edern (second) et Jean (le dernier). Elle veut que l'aîné ait 20 € de plus que le second et que le ssecond ait 10 € de plus que le dernier. Quelle somme doit-elle donner à Edern ?
On pose l’équation suivante avec « x » la somme qui sera donnée au dernier enfant :
160 = (x + 20 + 10) (x + 10) + x
160 = 3x + 40
x = (160 – 40) / 3 = 40 euros
Jean reçoit 40 euros, Edern reçoit 40 + 10, soit 50 euros et Orène reçoit 40 + 20, soit 60 euros.
#58. Un ruban fait 80 cm de long. 2/5 de sa longueur sont coupés. 25 % de sa longueur restante sont également coupés. Quelle longueur de ruban reste-t-il ?
Un ruban fait 80 cm de long
2/5 de sa longueur sont coupés = 80cm x (2/5) = 32 cm ; il reste 80cm – 32cm = 48 cm
25 % (soit ¼) de sa longueur restante sont également coupés = 48cm x ¼ = 12 cm
Il reste 48cm – 12cm = 36 cm.
#59. Après remise de 30 %, le prix payé est de 210 €. Quel est le montant de la remise ?
Après remise de 30 %, le prix payé est de 210 € (soit 70% de la somme totale initiale)
Ainsi, le prix initial = (210 x 100) / 70 = 300 euros.
La remise est donc de 300 – 210 = 90 euros ou 300 x 0,30 = 90 euros
#60. Pierre et Jean vont régulièrement à la patinoire. Deux tarifs sont proposés : Tarif 1 : 8,80 € l'entrée Tarif 2 : Une carte d'abonnement à 15 € puis l'entrée à 6,30 € Pierre prend le tarif 1 et Jean prend le tarif 2. Pour quel nombre d'entrées auront-ils payé le même montant ?
Pierre : Tarif 1 : 8,80 € l’entrée
8,80×2 = 17,60 euros
8,80×3 = 26,40 euros
8,80×6 = 52,80 euros
Jean : Tarif 2 : Une carte d’abonnement à 15 € puis l’entrée à 6,30 €
15 + 6 ,30×2 = 27,60 euros
15 + 6,30×3 = 33,90 euros
15 + 6,30×6 = 52,80 euros
#61. Quelle affirmation est juste ?
#62. Le nombre entier 58 680 est :
58 680/3 = 19 560
58 680/5 = 11 736
58 680/2 = 29 340
#63. Une horloge sonne toutes les heures (exemple : elle sonne quatre coups à 4h et à 16h) et sonne un coup à chaque demi-heure. Combien de coups sonne-t-elle en 24 heures, sachant qu’elle mentionne un retard de 6 minutes par rapport à l’horloge universelle ?
L’horloge sonne chaque heure un nombre de coups équivalent au chiffre indiqué sur le cadran soit : 1×2+ 2×2+ 3×2+ 4×2+ 5×2+ 6×2+ 7×2+ 8×2+ 9×2+ 10×2+ 11×2+ 12×2 = 156 fois
Il faut ajouter un coup donné chaque demi-heure ; en une journée, il y a 24h et donc 24 demi-heures = 24 coups pour chaque demi-heure
Soit 156 + 24 = 180
#64. Dans une salle de cinéma, les enfants paient demi-tarif et les adultes paient plein tarif. Deux adultes et cinq enfants ont payé au total 51,50 euros. Combien paiera un groupe composé de quatre adultes et dix enfants ?
Un groupe de 4 adultes et 10 enfants paiera 2 fois plus cher que le groupe composé de 2 adultes et 5 enfants soit 51,50 x 2 = 103 euros
#65. Dans une urne, il y a 9 boules indiscernables au toucher et qui portent chacune un numéro : 1 – 5 – 2 – 3 – 5 – 4 – 5 – 9 – 6 . Parmi les évènements ci-dessous, quel est celui qui a la plus forte probabilité de survenir ?
J’ai 3 chances sur 9 de tirer une boule avec un n° pair
J’ai 6 chances sur 9 de tirer une boule avec un n° impair
J’ai 4 chances sur 9 de tirer une boule avec un n° premier
J’ai 3 chances sur 9 de tirer une boule n°5

#66. 30 élèves d’une même classe ont composé sur un sujet de mathématiques. Leurs notes figurent dans le tableau ci-dessus. Quel est la moyenne de la classe ?
La moyenne de la classe correspond à la somme de l’ensemble des notes divisée par le nombre d’élèves ayant composé sur le sujet de mathématiques :
(2×0 + 1X1 + 3X2 + 4X4 + 5X8 +6X5 + 7X4 + 8X2 + 9X1 + 10X1) / 30 = 5,20
#67. Les solutions de l’équation (6x-2)(x+6)=0 sont :
(6 x 1/3 – 2)(- 6 + 6) = 0
(2 – 2)(-6 + 6) = 0
0 x 0 = 0
#68. Les trois hauteurs d’un triangle sont concourantes en un point appelé :
#69. En développant (4x-5)(4x-5) on obtient :
(4x-5) (4x-5)
= 16x² – 20x – 20x + 25
= 16x² – 40x + 25
#70. Si on triple la longueur du côté d’un carré, son aire est multipliée par :
Prenons un exemple : un carré à des côtés de 2 cm
L’aire du carré = côté x côté = 2 x 2 = 4
Si on triple le côté du carré = 3 x 2 = 6
Donc l’aire du nouveau carré est de : 6 x 6 = 36
L’aire a donc été multipliée par 9 (4 x 9 = 36)
#71. Quelle est la fraction irréductible de 192/288 ?
192 / 288 = 2×96 / 3×96
En simplifiant on obtient 2/3
#72. Lors d’un contrôle de vitesse, 350 véhicules étaient en infraction parmi les 1 400 véhicules contrôlés. Quel est le pourcentage de véhicules respectant la vitesse autorisée ?
1400 véhicules contrôlés = 100%
350 = X % (véhicules ne respectant pas la vitesse)
1050 = Z % (véhicules respectant la vitesse)
X = 350 x 100 / 1400 = 25%
Z = 100 – 25 = 75 % ou 1050 x 100 / 1400 = 75%
#73. Quel est le double du cube de 2
Le cube de 2 = 2x2x2 = 8
Le double du cube de 2 = 2×8 = 16
#74. Sachant qu’un bassin a une longueur de 3 m, une largeur de 2 m et une profondeur de 0,54 m, combien faut-il de m^3 d’eau pour le remplir ?
Volume du bassin = L x l x p
L = 3m
l = 2m
p = 0,54m
soit : 3 x 2 x 0,54 = 3,24
#75. Un placement financier d’une valeur de 250 000 euros vaut 266 250 euros l’année suivante. Quel est le taux d’intérêt de ce placement ?
266250-250000 =16250
16250/250000*100 = 6.5%
#76. 18 ouvriers travaillant 8 heures par jour ont pavé en 10 jours une rue longue de 150 mètres. Combien faudrait-il d’ouvrier travaillant 6h par jour pour paver en 15 jours une rue de 75 mètres de long ?
Réponse 2
Les ouvriers travaillent 8h/j pendant 10 jours, soit 80 heures (8×10).
En 80h, 18 ouvriers ont pavé 150m.
Soit 150 / 80 = 1,875 m / h
Et donc 0,104 m par ouvrier et par heure.
Si les ouvriers travaillaient 6h/j pendant 15 jours, cela fait un total de 90h.
Ainsi, 0,104 x 90 = 9,36 m par ouvrier
75 / 9,36 = 8 ouvriers.
#77. Factorisez F(x) = x^2 – 10x + 25
#78. Déterminez l’équation réduite de la droite passant par les points A(3 ;-1) et B(2 ;0)
#79. Un premier cycliste part de Lyon à 8h et se dirige vers Marseille à la vitesse constante de 25km à l’heure. A 10h, un second cycliste part du même point, prend la même direction à la vitesse constante de 40km à l’heure. A quelle heure le second cycliste aura-t-il rejoint le premier ?
Réponse 2
Cycliste 1 : à 10h il a parcouru 50km ; à 11h, 75km ; à midi 100 km ; à 13h, 125 km ; à 14h 150km
Cycliste 2 : à 10h, il a parcouru 0 km ; à 11h, 40km ; à midi 80 km ; à 13h, 120 km ; à 14h 160km
#80. Je lance trois dés numérotés de 1 à 6, quelle est la probabilité de tomber sur un nombre premier pair en additionnant la somme des trois dés ?
Réponse A : Aucune des réponses n’est correcte
2 est le seul nombre premier pair. Par conséquent, en additionnant la somme des 3 dés il est impossible de trouver le chiffre 2.
#81. Quelle est l’aire d’un trapèze dont les mesures sont : B = 300 mm ; b = 20 cm et h = 0,8 dm ?
Réponse 4
L’aire A d’un trapèze dont les bases sont b et B et dont la hauteur est h est : A=(B+ b)×h2.
Soit A = (30+ 20) x 8/2 = 200cm^2
#82. Une voiture voit successivement son prix augmenter de 20% puis baisser de 20%. Quelle affirmation est vraie ?
Réponse 2
Prenons un exemple chiffré : le prix est de 1000 euros
Augmentation de 20 % = 1200 euros (1000 x 1,20)
Diminution de 20 % = 960 euros (1200 x 0,80)
Le prix a donc diminué de 4%
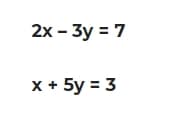
#83. Résolvez le système d’équations :
Réponse 1 :
Résolution de l’équation par substitution :
- Trouver x :
2x – 3y = 7 devient 10x – 15y = 35 (multiplication par 5 de l’équation)
x 5y = -3 devient 3x 15y = -9 (multiplication par 3 de l’équation)
10x Р15y 3x 15y = 35 Р9 (on descend lӎquation du haut dans celle du bas)
13x = 26
x= 26/13
x = 2
- Trouver y :
2x – 3y = 7 devient 2 x 2 – 3y = 7
4 – 3y = 7
-3y = 7 – 4
-3y = 3
-3y/-3 = 3/-3
y = -1
#84. Une machine produit 100 unités à la minute. Si 24 unités peuvent être emballées dans une caisse, combien de caisses la machine peut-elle remplir en une heure ?
Réponse 2
100 unités / minute, soit 6000 unités / heure
1 caisse contient 24 unités
Les 6000 unités seront emballées dans 250 caisses : 6000 (nombre total d’unités produites en 1h) / 24 (nombre d’unités contenues dans une caisse) = 250 caisses
#85. Combien représentent sur le terrain 3 centimètres sur une carte au 1/25 000ème ?
Réponse 3
3 cm représentent 1/25 000ème, donc sur le terrain ils représentent 750m.
#86. Considérons la Lune comme une sphère de rayon R égal à 17. Quelle est sa superficie ? PI est égal à 3.
Réponse 3
La formule pour savoir comment calculer l’aire d’une sphère est : 4 × π × R^2.
Soit 4 x 3 x 17^2 = 3 468
#87. Combien représente sur le terrain 4 centimètres sur une carte à l’échelle 1/250 000 ?
Réponse 1 : 1 cm sur la carte = 250 000 cm en réel donc 4 cm sur la carte = 4 x 250 000 soit 1 000 000 cm en réel, c’est-à-dire 10 km.
#88. Soit un triangle rectangle dont les longueurs des côtés de l’angle droit mesurent 3 et 4 cm. Quelle est la longueur de l’hypoténuse ?
Réponse 1 : l’hypoténuse est le côté opposé à l’angle droit
On applique le théorème de Pythagore : pour un triangle rectangle dont les côtés adjacents à l’angle droit sont a et b et l’hypoténuse est c, on a : a2 + b2= c2 , soit 9 + 16 = 25 et donc C = 5 cm
#89. Quel est le montant hors taxe d’un produit dont le prix de vente est de 422 euros avec un taux de TVA de 5,5 % ?
Réponse 4 : TTC = 422 euros ; TVA = 5,5 % ; HT = TTC / 1 + TVA = 422 /1,055 = 400 euros
#90. Jean a acheté une voiture qui consomme 6 litres aux 100 km en ville et 8 litres aux 100 km sur autoroute. Pendant un voyage, Jean a utilisé 135 litres pour parcourir une distance totale de 1 800 km. Combien de kilomètres a-t-il parcouru en ville ?
Réponse 3 :
135 L => 1 800 km et 7,5L => 100 km
En moyenne, pendant le voyage, la consommation de carburant est de 7,5L/100km.
1/ 250 km en ville, 6L => 100 km et 15 L => 250 km
Ainsi, 8L = 100 km et 124 L = 1550 km : la proposition n°1 est fausse
2/ 350 km en ville, 6L => 100 km et 21 L => 350 km
Ainsi, 8L = 100 km et 116 L = 1450 km : la proposition n°2 est fausse
3/ 450 km en ville, 6L => 100 km et 27 L => 450 km
Ainsi, 8L = 100 km et 108 L = 1350 km ; 108 + 27 = 135 L donc la proposition n°3 est vraie !
#91. Quel est le quart de (5 + 41 x 3 ) ?
Réponse 1 : (5 + 41 x 3 ) = (5 + 123) = 128 ; 128/4 = 32
#92. Quelle est la probabilité d’obtenir 3 en lançant deux dés ont on fait la somme ?
Réponse 2 : chaque dès a 6 faces ; la probabilité de tomber sur la face 3 est de 1/36 ; la probabilité que les deux dès tombent sur la face 3 en même temps est de : 2 x 1/36 = 1/18
#93. Dans une assemblée de 500 personnes, il y a 36 % de femmes, 25 % de ces femmes ont plus de 50 ans. Combien de femmes dans cette assemblée ont plus de 50 ans ?
Réponse 2 : l’assemblée de 500 personnes comporte 180 femmes (500 x 36 / 100 = 180). Parmi ces 180 femmes, 25 % ont plus de 50 ans, soit : 180 x 25 / 100 = 45.
#94. Pour scier un tronc d’arbre en 5 morceaux, Paul met 3 minutes et 8 secondes. Combien de temps lui faudra-t-il pour couper ce tronc en 10 morceaux ?
Réponse 2 : couper un tronc en 5 morceaux nécessite de faire 4 coupes ; en 10 morceaux, 9 coupes.
Pour 4 coupe, il faut 188 secondes
Pour 1 coupes, il faut 47 secondes
Pour 9 coupes, il faut 47 x 9 = 423 secondes, soit 7 minutes et 3 secondes
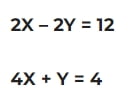
#95. Résolvez le système d’équations ci dessus
Réponse 4 : il faut isoler une inconnue dans l’une des équations puis remplacer cette inconnue dans la seconde équation.
2X – 2Y = 12
=> 2X = 12 + 2Y
=> X = (12 + 2Y) / 2
=> X = 6 + Y
Donc 4X + Y = 4 signifie 4 (6 + Y) + Y = 4
=> 24 + 4Y + Y = 4
=> 5Y = – 20
=> Y = – 4
Bilan : { X=2 ; Y = -4 }
#96. Une parachutiste saute d’une altitude de 4 000 mètres. En chute libre, sa vitesse est de 200 km/heure. Il ouvre son parachute à 1 500 mètres d’altitude. Sa vitesse est alors de 20 km/heure. Combien de temps dure son saut ?
Réponse 2 :
Calcul vitesse chute libre : 4000 – 1500 = 2500m à 200km/h, soit 200 km en 3600 secondes ou 2 km en 36 secondes => 2500 m en 45 secondes.
Calcul vitesse avec parachute : 1500m à 20km/h, soit 20 km en 60 minute ou 1 km en 3 minutes => 1500 m en 4,5 minutes, c’est-à-dire 4 minutes et 30 secondes.
Calcul temps total : 45 secondes + 4 minutes et 30 secondes = 5 mn et 15 secondes
#97. Quelle est la forme factorisée de (5x – 4) (x – 1) – (5x – 4)² ?
Réponse 3 :
(5x – 4) (x – 1) – (5x – 4) 2
=> (5x – 4) (x-1) – (5x – 4) (5x-4)
=> (5x – 4) [(x – 1) – (5x – 4)
=> (5x – 4) (-4x + 3)
#98. Voici les temps (en secondes) de la finale de 100m femmes des Jeux Olympiques de Rio de 2016 : 10,86 – 11,80 – 10,83 – 10,90 – 10,94 – 10,71 – 10,92 – 10,86. Quel est le temps médian de cette course ?
Réponse 3 : La médiane est l’élément central au-dessus et en dessous duquel se situent 50 % des autres éléments.
Il est possible de ranger les éléments dans l’ordre croissant pour trouver la médiane :
10,71 – 10,83 – 10,86- 10,86 – 10,90 – 10,92 – 10,94 – 11,80
La médiane = (10,86 + 10,90) / 2 = 10,88
#99. Un commerçant met en vente une chaise, dont le prix hors taxe est de 120 euros. La TVA applicable est de 20%. Quel sera le prix payé par un client pour acquérir cette chaise, sachant que le commerçant consent à une remise exceptionnelle de 10 %.
Réponse 2 : prix de la chaise TTC = 120 x 120 / 100 = 144 euros.
Le client bénéficie en plus d’une remise de 10 %, soit 144 – 10% = 144 – 14,40 = 129,60 euros.
#100. – 4 est la solution de :
Réponse 4 : – 4 x – 4 = 16 ; donc x^2 – 16 = 16 – 16 = 0

#101. ADB est un triangle isocèle, rectangle en D. ABC est un triangle isocèle, rectangle en B. BD = 8 cm Calculez AC.
Réponse : 4
Un triangle isocèle à deux côtés égaux : ici, AD = DB et AB = BC
AB^2 = AD^2+DB^2 = 8^2+8^2 = 64+64 = 128 cm2
AC^2 = 128+128 = 256 cm2
√256 = 16 cm
#102. Une agente travaille 35 heures par semaine réparties équitablement sur 5 jours. Quels peuvent être ses horaires ?
Réponse 2
1. 8h15 à 12h00 et 14h00 à 17h00 : 3h45 + 3 = 6h45 x 5 jours = 33h45.
2. 8h30 à 11h45 et 13h15 à 17h00 : 3h15 + 3h45 = 7 x 5 jours = 35 heures
3. 8h00 à 12h00 et 13h45 à 17h15 : 4h + 3h30 = 7h30 5 jours = 37h30
4. 8h15 à 12h15 et 13h45 à 17h45 : 4h + 4h = 8h x 5 jours = 40 heures
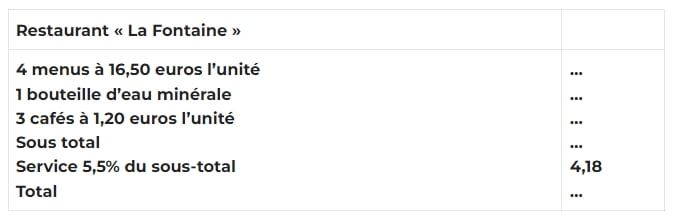
#103. La note de restaurant ci-dessus est partiellement effacée. Quel est le prix de la bouteille d’eau minérale ?
Réponse 3
4 menus à 16,50 euros l’unité = 4 x 16,50 = 66 euros
3 cafés à 1,20 euros l’unité = 3 x 1,20 = 3,60 euros
5,5% du sous total = 4, 18 euros et donc sous total = 4, 18 x 100 / 5,5 = 76 euros
1 bouteille d’eau minérale = 76 – 3,60 – 66 = 6,40 euros.
#104. Quel est le résultat de l’opération suivante : 1-2x(3+5)
Réponse A : aucune des réponses n’est correcte
Il faut additionner les chiffres entre parenthèses : 3+5 = 8
2 x (3+5) = 2 x 8 = 16
1 – 2 x (3+5) = 1 – 2 x 8 = 1 – 16 = – 15
#105. Quelle est la fraction irréductible de 84/245 ?
Réponse 3
84 / 7 = 12
245 / 7 = 35
Donc 84/245 = = 12 x 7 / 35 x 7 = 12/35
#106. 5 élèves ont respectivement 06/20, 08/20, 12/20, 16/20 et 20/20 à un devoir de français. Quelle affirmation suivante est vraie ?
Réponse 3
La médiane est la valeur qui sépare en deux parties la moitié inférieure de la moitié supérieure
Ici, la médiane = 12/20 et la moyenne = 12,40
#107. Quelle est l’aire d’un carré de 7 cm de côté ?
Réponse 4 : aire d’un carré = côté x côté = 7 x 7 = 49 cm2
#108. Combien y-a-t-il de minutes dans le second semestre d’une année ?
Réponse 3 : il faut déterminer le nombre de minutes pour les 6 derniers mois d’une année
Juillet-août- septembre-octobre-novembre-décembre
Nombre de jours : 31+31+30+31+30+31 = 184 jours
Nombre de minutes en une journée = 24 heures x 60 = 1440 minutes
Nombre de minutes pour le second semestre = 184 x 1440 = 264 960
#109. Kévin a 10 ans. Son petit frère Léo a la moitié de son âge. Quand Kévin sera 10 fois plus âgé, quel âge aura Léo.
Réponse A : aucune des réponses n’est correcte
Kévin a 10 ans. Son petit frère Léo a la moitié de son âge, soit 5 ans. Quand Kévin sera 10 fois plus âgé, il aura 100 ans, Léo aura 100 – 5 = 95 ans.
#110. Jasmine a acheté 5 croissants et a payé 5,75 euros. Quel est le prix d’un croissant ?
Réponse 2 : 5,75 / 5 = 1,15 euros


